你的孩子會學什麼
看看第4年(8-9歲)在國家課程期望的期望:
知道最多12×12的時間表
期望您的孩子知道他們所有的時間桌,最多可達12×12。他們將使用這些知識來解決乘法問題並解決相關的分區事實(例如,如果7×8 = 56, 然後56÷7 = 8)。
使用位置價值和數字事實在精神上解決問題
您的孩子應該能夠使用乘法事實來解決分裂計算,並有望使用已知事實以最多三位數的數字來計算精神。例如,600÷3 = 200可以通過知道2×3 = 6。
他們還將學會將三個數字倍增(例如,3×4×5 = 60)。
在心理計算中使用因子對和通勤性
將兩位數和三位數的數字乘以一位數的數字
您的孩子將繼續練習正式的乘法和分裂方式。他們將使用這些形式的方法來解決涉及兩位數和三位數數字乘以一位數數字的計算(例如,73×6和637×8)。
他們將練習正式的簡短乘法和短劃分的書麵方法,其答案是全數字。
如何在家幫助
有很多快速簡便的方法可以幫助您的孩子了解乘法和分裂。這裏隻是支持孩子學習的一些想法:
1.在現實生活中找到乘法事實
您可以使用日常情況來練習乘法事實。例如,如果您在超市,並且購買了三包多包薯片,每個薯片中有6個包裝,您可以問孩子總共有多少包薯片。討論他們使用的計算。
如果您的孩子立即知道答案,請問他們他們知道的其他數字事實,如果他們知道3×6 = 18。例如,他們可能知道18÷6 = 3或者那個18÷3 = 6。
2.使用不同的乘以數字的方式
鼓勵您的孩子使用許多方法來乘以數字,並使用他們的理解:
- 加倍和減半。例如,如果我們知道2×6 = 12,那麼我們也知道4×6 = 24,,,,8×6 = 48, 等等。
- 換算性(即,知道我們可以按任何順序完成乘法總和,並達到相同的答案)。例如,如果我們知道2×6 = 12,那麼我們也知道6×2 = 12。
- 逆操作。例如,如果我們知道2×6 = 12,那麼我們也知道12÷2 = 6和12÷6 = 2。
- 位置值。例如,如果我們知道20×6 = 120,那麼我們也知道200×6 = 1200,,,,2×0·6 = 1·2, 等等。
鼓勵您的孩子對與乘法事實2×6 = 12有關的所有事實製作思維地圖。他們可能會對他們從一個計算中鍛煉多少感到驚訝!
區域/網格法
將教您的孩子在學校解決乘法問題的一係列方法,例如使用物理資源,圖紙和圖表,例如區域/網格方法。bwin国际娱乐以示例65×74:
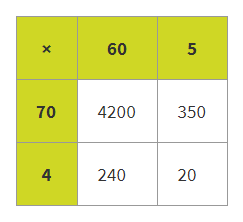
在網格方法中,您的孩子將分區(分解)將乘以的每個數字。在此示例中,它們將每個數字分為TENS和一個-65分為60和5,將74分為70和74。然後,他們將在將所有值添加在一起之前找到每對數字的乘積:
70×60 = 4200
70×5 = 350
4×60 = 240
4×5 = 20
4200 + 350 + 240 + 20 =4810
您的孩子還將期望使用正式的書麵方法,例如短乘法。通過練習許多不同的數字方式,您可以幫助您的孩子在思維中獲得信心和靈活性。這將使他們在任何給定情況下選擇最佳方法。
3.玩1到21場比賽
您可以通過玩1到21場比賽來幫助孩子在家中練習所有四項操作。
要求他們擲骰子五次,並記錄一張紙上骰子上顯示的每個數字。例如,1、4、3、5、3。然後,他們需要在數字上使用任何操作(加法,減法,乘法和/或分裂)找到一種方法來達到1的答案。
您的孩子隻能使用每個數字一次,他們必須在每個計算中使用至少兩個數字。例如,我們可以通過計算3÷3、5-4、4-3等來獲得1的答案。然後,請您的孩子使用任何操作找到2個答案的計算,然後回答3,依此類推,直到他們達到21。
您可以說他們必須使用至少三個,四個甚至所有五個數字才能使它變得非常棘手,從而使這款遊戲更具挑戰性!打印出我們的活動表,以便進行:
活動:一到二十一

找到使所有數字1到21的方法。
4.談論因素和倍數
嚐試幫助您的孩子識別這些詞並在談論乘法和分裂時使用這些單詞:
- 因素- 一個可以乘以另一個整數以使特定的第三個數乘以的整數。例如,1、2、3、6、9和18都是18的因素。
- 因子對- 這些數字成乘以其他數字。例如,6和3是18個因子對。另一個因子對18是9和2。
- 常見因素- 共同因素是兩個數字共同的因素。例如,12的因素為1、2、3、4、6和12。8的因素為1、2、4和8。因此,12和8的共同因素為1、2和24。